학습개요
데이터로부터 의미 있는 정보를 얻기 위한 첫 단계는 데이터를 요약하여 특성을 파악하는 것입니다. 데이터를 이루는 변수의 종류와 분포의 특성에 따라 적합한 방법으로 데이터를 요약해야 합니다. 이 장에서는 변수의 종류를 알아보고, 질적 데이터를 요약하는 막대그래프에 대하여 알아봅시다. 또한 R에서 ggplot2 패키지를 설치하여 막대그래프를 그리는 방법을 실습해봅시다.
학습목표
1. 변수의 종류를 구분할 수 있습니다.
2. 데이터로부터 변수의 분포를 도수분포표로 요약할 수 있습니다.
3. R을 이용하여 막대그래프를 그릴 수 있습니다.
주요용어
- 도수분포표(frequency table) : 데이터에서 각 값의 출현빈도나 비슷한 값끼리 묶은 구간별로 관측된 데이터의 개수를 정리한 표
- 질적 변수(qualitative variable) : 유한개의 범주 중 하나의 값을 취하는 변수로, 범주형 변수
- 양적 변수(quantitative variable) : 양적인 수치로 측정되는 변수
2.1. 변수
제 1장에서 살펴본 바와 같이 변수는 각 단위에 대해 관측되는 특성이고, 데이터는 하나 이상의 변수로 구성되어 있습니다. 데이터를 이해하기 위해서는 그 데이터를 구성하고 있는 각 변수의 특성과 변수들 간의 관계를 살펴보아야 합니다.
1) 변수의 종류
변수는 크게 질적 변수와 양적 변수로 구분됩니다. 질적 변수는 범주형 변수라고도 하는데, 유한개의 범주 중 하나의 값을 취하는 변수입니다. 즉, 각 단위가 유한개의 범주 중에 어떤 범주에 속하는지를 나타내는 변수라고 볼 수 있습니다.
질적 변수의 값으로 취할 수 있는 범주들이 의미 있는 순서를 정할 수 없는 경우에는 명목형 변수, 범주 간의 순서가 의미 있는 경우에는 순서형 변수라고 합니다. 예를 들어, 성별(여성, 남성), 혈액형(A, B, AB, O) 등은 범주들 간에 크고 작은 개념이 적용되지 않아 순서의 의미가 없으므로 명목형 변수입니다. 그러나 암의 병기(1기, 2기, 3기, 4기), 교육수준(초졸, 중졸, 고졸, 대졸 이상) 등과 같은 변수는 범주들 간에 뚜렷한 순서가 있으므로 순서형 변수라고 할 수 있습니다. 질적 변수의 값은 범주이기 때문에 사칙연산을 적용할 수 없습니다. 예를 들어, 혈액형이 A형인 사람과 AB형인 사람의 "평균" 혈액형이라는 것은 의미가 없습니다. 마찬가지로 암의 병기가 1기인 환자와 2기인 환자 2명의 병기를 합해서 3기라는 계산은 아무 의미가 없습니다.
양적 변수는 양적인 수치로 측정되는 변수를 의미합니다. 양적 변수는 다시 연속형 변수와 이산형 변수로 나뉩니다. 연속형 변수는 어떤 실수 구간 안의 모든 값을 가직 수 있습니다. 몸무게, 키, 온도와 같이 일정 범위 안의 어떤 값이라도 가질 수 있는 연속형 변수는 취할 수 있는 값을 모두 세는 것이 불가능합니다. 예를 들어, 몸무게는 60㎏, 61㎏, 60.1㎏, 60.000001㎏ 등 여러 경우가 있으므로 가능한 값을 모두 세는 것이 불가능합니다. 반면 이산형 변수는 변수가 취할 수 있는 값을 셀 수 있는 변수입니다. 예를 들어, 가구당 아동의 수, 1분 안에 할 수 있는 윗몸일으키기 횟수, 기말고사 수학점수 등은 모두 이산형 변수입니다.
경우에 따라서는 같은 변수라도 연속형 변수 또는 이산형 변수로 취급될 수 있습니다. 예를 들어, 몸무게는 위에서 살펴본 바와 같이 취할 수 있는 값이 셀 수 없을만큼 다양하지만, 몸무게를 디지털 체중계로 측정하여 0.1㎏ 단위까지만 기록한다면 가능한 몸무게 값의 개수를 셀 수 있게 되므로 이산형 변수라고 볼 수 있습니다.
| 질적 변수(qualitative variable) 유한개의 범주 중 하나의 값을 취하는 변수로, 범주형 변수라고도 합니다. • 명목형 변수(nominal variable) : 범주들에 의미 있는 순서를 정할 수 없는 질적 변수 • 순서형 변수(ordinal variable) : 범주 간의 의미 있는 순서를 정할 수 있는 질적 변수 양적 변수(quantitative variable) 양적인 수치로 측정되는 변수입니다. • 연속형 변수(continuous variable) : 어떤 실수 구간 안의 모든 값을 가질 수 있는 변수 • 이산형 변수(discrete variable) : 취할 수 있는 값을 셀 수 있는 양적 변수 |
2) 변수의 분포
몸무게라는 변수의 값은 어떤 사람에게서 관찰하느냐에 따라 값이 다릅니다. 성별이라는 변수 역시 애초에 여성 또는 남성으로만 구성된 모집단을 대상으로 관찰한 것이 아니라면, 관측 단위에 따라 값이 달라집니다. 즉, 극히 예외적인 경우를 제외하고는 변수의 값은 관측 단위에 따라 값이 달라집니다. 즉, 극히 예외적인 경우를 제외하고는 변수의 값은 관측 단위에 따라 달라집니다. 다시 말하면, 어떤 변수에 대해 측정된 데이터에는 변동(variability)이 있다고 할 수 있습니다. 어떤 변수의 변동을 표현하기 위해, 그 변수가 취할 수 있는 모든 값에 대해 각 값이 발생하는 빈도를 나열한 것을 변수의 분포라고 합니다. 이때, 각 값이 발생하는 빈도를 합이 1인 확률로 나타내는 것을 확률분포라고 합니다.
우리는 모집단에서의 변수 분포를 파악하기 위해 모집단에서 표집한 표본의 데이터를 가지고 관심 변수의 분포를 추정합니다. 많은 경우 표본 데이터 자체는 양이 많기 때문에 요약, 정리하지 않으면 분포를 쉽게 파악할 수 없습니다. 따라서 변수의 분포를 쉽게 파악할 수 있도록 데이터에서 각 값의 출현빈도나 비슷한 값끼리 묶은 구간별로 관측된 데이터의 개수를 정리한 표를 만들면 유용합니다. 이러한 표를 도수분포표라고 하며, 이것은 표본 데이터에서 관측된 변수의 분포를 요약하는 가장 기본적인 방법입니다. [예제 2-1]과 [예제 2-2]는 도수분포표의 예입니다.
[예제 2-1] 한국방송통신대학교 통계·데이터과학과에서 2020년 재학생을 대상으로, 한국방송통신대학교를 선택한 이유에 대해 설문조사를 실시하여 다음과 같은 도수분포표로 요약했습니다.

[예제 2-2] 한 체육관에서 회원들의 몸무게를 측정하여 다음과 같은 도수분포표로 요약했습니다.

[예제 2-1]과 같은 질적 변수에 대한 도수분포표는 변수가 취할 수 있는 각 범주마다 관측된 관측 단위의 개수를 제시하면 되므로 비교적 간단하게 만들 수 있습니다. [예제 2-2]와 같은 양적 변수에 대한 도수분포표를 만들 때는 계급(class)을 어떻게 만들지 정해야 합니다. 각 계급의 폭과 계급 사이의 경계점은 임의로 정할 수 있으나, 특별한 이유가 있을 경우를 제외하고는 각 계급의 폭을 일정하게 하는 것이 좋습니다. 계급의 폭을 너무 좁게 잡으면 계급의 개수가 너무 많아지거나 각 계급의 도수가 너무 작을 수 있으며, 폭을 너무 넓게 잡으면 전체적인 분포가 잘 드러나지 않을 수도 있습니다. 그리고 되도록이면 각 계급의 경계점에 놓이는 관찰값의 개수가 적어지도록 계급을 정하는 것이 좋습니다.
도수분포표는 각 계급의 도수, 즉 각 계급에 속하는 관찰값의 개수만 보여 줄수도 있고, [예제 2-2]의 경우와 같이 상대 도수, 즉 각 계급의 속하는 관찰값의 비율을 같이 보여 줄 수도 있습니다.
2.2. 질적 데이터의 요약
질적 변수의 분포를 알기 위해 그래프를 이용하여 표본으로 모은 질적 데이터를 요약하는 방법을 알아봅시다. 질적 데이터에 대한 그래프는 막대그래프(bar graph, bar plot)가 널리 사용됩니다. 막대그래프는 각 범주에 속한 관찰값의 개수 또는 비율을 막대의 길이로 나타낸 것입니다.
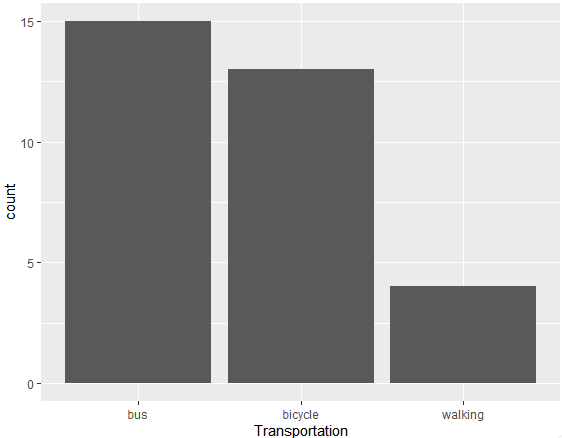
[예제 2-3] 다음은 어느 고등학교 학습의 학생들을 대상으로 등하교 교통수단을 조사한 막대그래프입니다. 버스를 타고 다니는 학생이 15명으로 가장 많고, 다음으로 자전거를 타고 다니는 학생이 많으며, 소수의 학생이 걸어다닌다는 것을 알 수 있습니다.
# 패키지 로드
library(ggplot2)
library(forcats)
# 데이터 입력
transp<-c("bicycle","bus","bus","walking","bus","bicycle","bicycle",
"bus","bus","bus","bicycle","bus","bicycle","bicycle",
"walking","bus","bus","bicycle","bicycle","walking","walking",
"bicycle","bus","bus","bus","bus","bicycle","bus","bus",
"bicycle","bicycle","bicycle")
dat1<-data.frame(transp)
# 막대그래프 작성
ggplot(data=dat1)+geom_bar(mapping=aes(x=fct_infreq(transp)))+
xlab("Transportation")
그래프를 그리는 데 필요한 ggplot2 패키지와, 막대그래프에서 범주의 순서를 바꾸는 데 유용한 함수 fct_infreq( )를 내장한 forcats 패키지를 설치한 후 위의 코드를 실행합니다. 1행과 같이 # 표시가 있는 명령어는 # 이후에 나온 부분이 실행되지 않습니다. 따라서 프로그램에 간단한 설명이나 제목을 달 경우에는 # 표시를 하고 필요한 내용을 적어주면 됩니다.
5~9행에서는 그래프를 통해 나타내려는 원 데이터를 transp라는 객체에 저장합니다. ggplot2 패키지를 이용하여 그래프를 그릴 때는 ggplot( )+geom 함수의 형태를 취해야 합니다. ggplot( ) 함수 안에는 'data='구문으로 그래프를 그릴 데이터세트 이름을 지정합니다. geom 함수에는 여러 종류가 있는데, 이 예제에서는 막대그래프를 그리기 위해 geom_bar( ) 함수를 사용했습니다. geom_bar( ) 안의 mapping=aes( ) 안에 'x=' 구문으로 그래프를 그릴 변수 이름을 입력합니다. geom_bar(mapping=aes(x=transp))으로 입력해도 막대그래프를 그릴 수 있으나, 빈도수가 높은 교통 수단부터 낮은 교통수단 순서로 보여 주기 위하여 fct_infreq( ) 함수를 사용했습니다.
ggplot2 패키지를 이용할 때는 기본적인 ggplot( )+geom 함수 형태 뒤에 + 표시로 추가적인 요소를 덧붙일 수 있습니다. 위에서는 xlab( ) 함수를 덧붙여 수평축의 이름을 지정해 주었습니다.
[예제 2-4] 다음은 어느 가정의학과 의원을 일주일 동안 방문한 환자들의 비만도 분포를 나타낸 막대그래프입니다.

# 데이터 입력
obesity<-factor(c("underweight","normal","overweight","obese"),
levels=c("underweight","normal","overweight","obese"))
count<-c(6,69,27,13)
perc<-count/sum(count)*100
dat2<-data.frame(obesity,count,perc)
# 막대그래프 작성
ggplot(data=dat2)+geom_bar(mapping=aes(x=obesity, y=perc),
stat="identity")+xlab("Obesity")+ylab("Percentage (%)")
[예제 2-4]에서는 앞의 [예제 2-3]과 달리 데이터가 이미 도수분포표 형태로 정리되어 있는 경우를 실습합니다. 5행은 빈도수로부터 비율을 퍼센티지로 계산하는 명령어입니다. 원 데이터가 아닌 도수분포표 형태로 정리된 데이터로 막대그래프를 그릴 때에는 8~9행과 같이 geom_bar( ) 함수 안에 stat="identity"라는 옵션을 지정해 주어야 하고, mapping=aes( ) 구문 안에서 x에는 범주 이름을 가지고 있는 변수를, y에는 각 범주별 도수를 담고 있는 변수를 지정해 주어야 합니다.
범주 간에 순서가 없는 명목형 변수를 요약할 때는 큰 빈도부터, 작은 빈도, 또는 작은 빈도부터 큰 빈도의 순서로 정렬하여 그래프로 나타내면 보다 효율적으로 데이터를 파악 할 수 있습니다. 범주 간에 순서가 있는 순서형 변수의 경우, 범주의 순서를 지켜서 그래프를 그리는 것이 바람직합니다.
과거에 질적 데이터를 그래프로 표현할 때 많이 사용된 원그래프(pie chart)는 여전히 언론에서 선거 여론 조사 등의 데이터를 발표할 때 종종 사용됩니다. 그러나 원그래프에서 각 범주가 차지하는 면적을 눈으로 비교하는 것은 막대그래프에서 막대의 길이를 비교하는 것에 비해 정확도와 효율성이 떨어지기 때문에, 최근에는 원그래프보다 막대그래프를 선호하고 있습니다. [예제 2-5]는 원그래프의 한계점을 보여줍니다.
[예제 2-5] [예제 2-3]의 고등학생들의 등하교 교통수단 분포를 나타낸 원그래프입니다. 버스와 자전거 중 어느쪽을 이용하는 학생이 더 많은지 파악하는 것이 막대그래프에 비해 조금 어렵습니다.

# 도수분포표 형태로 데이터 정리
table(transp)
dat3<-data.frame(transportation=c("bus","bicycle","walking"),
count=c(15,13,4))
# 원 그래프 작성
ggplot(data=dat3)+geom_bar(mapping=aes(x="",y="",
fill=transportation), stat="identity")+theme_void()+
coord_polar("y",start=0)+xlab("")+ylab("")
데이터를 먼저 도수분포표 형태로 정리하고, 막대그래프가 아닌 원그래프를 그리기 위해 coord_polar( ) 함수를 덧붙였습니다.
2.2. R의 데이터 형태와 연산
R을 이용하여 통계 분석을 수행하려면 R에서 데이터가 다루어지는 방법에 대해 이해해야 합니다. 이 절에서는 R에서 데이터가 입력되고 저장되는 형태와 간단한 연산을 하는 방법에 대해 알아봅니다.
1) 객체의 생성과 저장
'1+2'라는 연산을 하는 가장 간단한 방법은 콘솔에 '1+2'를 입력하는 것입니다. 그러면 R은 3이라는 결과를 바로 출력합니다. 하지만 a라는 객체에 1을 저장하고, b라는 객체에 2를 저장한 후, a+b를 c에 저장할 수도 있습니다. 그러고 나서 c값을 출력하면 답을 얻게 됩니다. 이것을 실행하는 코드는 다음과 같습니다.
a<-1
b<-2
c<-a+b
c
R에서 '<-'와 '='는 대입 연산자로서, 이 기호의 오른쪽에 있는 값을 왼쪽의 객체에 저장합니다. 따라서 1행을 실행하면 R은 a라는 객체를 만들어 내고 그 객체에 1이라는 값을 저장합니다. 마찬가지로 2행에서 b라는 객체에 2라는 값을 저장하고, 3행에서 c라는 객체에 a+b의 값을 저장합니다. 4행과 같이 객체의 이름만 입력하면, 그 객체에 저장된 값이 출력됩니다.
객체의 이름은 대소문자를 구별하며, 특수문자는 쓸 수 없지만 밑줄(_)이나 마침표(.) 기호는 쓸 수 있습니다. 객체 이름의 첫 글자로 숫자나 밑줄은 쓸 수 없습니다. 한글로 객체의 이름을 쓰는 것도 가능하지만, 컴퓨터 환경에 따라서 오류가 날 수도 있으므로 영어로 쓰는 것이 편리합니다.
2) 벡터와 벡터의 연산
실제로 데이터 분석을 하다 보면 아래와 같이 단 하나의 값을 가지는 객체를 다루는 것보다는 여러 개의 값을 가지는 벡터 형태의 객체를 만들어 사용하는 것이 훨씬 유용합니다. 예를 들어 학생 10명의 키를 조사했다고 합시다. 이것은 키라는 변수의 관찰값 10개라고 볼 수 있습니다. 이것은 height라는 객체에 벡터 형태로 저장하는 명령어는 다음과 같습니다.
height<-c(165,151,162,160,151,152,159,163,143,161)
벡터를 생성하는 가장 기본적인 방법은 위와 같이 c( )라는 함수 안에 벡터의 각 요소를 쉼표로 구분하여 넣는 것입니다. 이 외에도 콜론을 이용하여 순차적으로 값이 1씩 증가하는 벡터를 만들 수도 있고, seq( ) 함수를 사용하여 초깃값과 종료값을 주고 그 사이를 일정 간격으로 증가하는 벡터를 만들 수도 있습니다. rep( ) 함수를 이용하면 같은 값이 여러 개 들어 있는 벡터를 만듭니다. 또한 이렇게 만든 벡터들을 c( ) 함수를 이용하여 결합할 수도 있습니다. 다음 코드를 R Studio에서 실행해 보고 결과를 관찰해 봅시다.
d<-1:3
d
e<-seq(1,9,2)
e
f<-rep(10,5)
f
g<-c(d,f)
g
h<-c(4:1, seq(0,9,3))
h

벡터들 간의 사칙연산도 가능합니다. 벡터의 길이가 같은 경우에는 각 벡터에서 같은 위치에 있는 숫자끼리 연산한 결과가 출력됩니다. 벡터의 길이가 다른 경우에는 길이가 짧은 벡터의 각 요소를 앞에서부터 재활용하면서 계산된 결과가 경고 메시지와 함께 출력됩니다. 아래 코드 실행 결과에 대해 살펴봅시다.
e+f
e-f
e*f
e/f
d+f

3) 데이터형
객체는 숫자만 저장할 수 있는 것이 아닙니다. 지금까지 본 양적인 값을 기닌 객체들을 양적 변수의 분석을 위해 사용한다면, 질적 변수의 분석을 위해 사용할 수 있는 범주형 객체도 있습니다. 이런 범주형 객체는 factor( ) 또는 as.factor( )라는 함수를 통해서 생성할 수 있으며, R은 범주형 객체의 값을 출력할 때 그 범주형 객체의 모든 범주를 levels라는 이름으로 같이 출력합니다. 또한 as.character( ) 함수를 이용하여 생성할 수 있는 문자형 객체도 있고, 참/거짓 값을 지니는 논리형 객체도 있습니다.
# 숫자형 벡터 객체
i<-1:4
# 범주형 벡터 객체
j<-as.factor(1:4)
j
# 숫자형 객체는 사칙연산이 가능
i+1
# 범주형 객체는 사직연산이 불가능
j+1
# 문자형 벡터 객체
k<-as.character(1:4)
k
l<-c("K","N","O","U")
l
# 논리형 객체
m<-i>2
m

9행에서 보듯이 범주형 객체는 사칙연산이 불가능하기 때문에, 범주형 객체에 연산을 적용하면 경고 메세지가 나오고 값은 NA로 출력됩니다. R에서 NA는 결측값 또는 계산할 수 없는 값을 나타낸다. 문자형 객체는 11행과 같이 as.character( ) 함수를 이용하여 생성할 수도 있고, 13행과 같이 직접 따옴표를 씌운 값을 입력하여 생성할 수도 있습니다. 문자형 객체의 값은 항상 따옴표가 씌워져서 출력됩니다. 16행은 i라는 객체의 각 요소가 2보다 크면 참(TRUE), 아니면 거짓(FALSE) 값을 생성하여 m이라는 객체에 저장하라는 뜻입니다. 이렇게 생성된 m은 논리형 객체입니다.
4) 행렬과 데이터 프레임
변수 여러 개가 모여서 데이터를 이루듯이, 벡터 여러 개가 모여서 행렬을 이룬다고 볼 수 있습니다. R에서는 cbind( ) 함수 또는 rbind( ) 함수를 이용하여 여러 개의 벡터를 묶어 행렬 형태의 객체를 만들 수도 있고, 처음부터 matrix( ) 함수를 이용하여 행렬 객체를 만들 수도 있습니다. 데이터형이 다른 벡터들은 하나의 행렬로 묶일 수 없습니다. 행렬 간의 연산도 가능한데, 특히 행렬의 곱셈은 %*% 연산자를 이용하여 계산이 가능하고, solve( ) 함수를 이용하면 역행렬도 구할 수 있습니다. 어떤 행렬의 i번째 행, j번째 열에 있는 요소를 출력하고 싶으면, 행렬 객체의 이름 옆에 [i, j]를 입력하면 됩니다. 행과 열 중의 하나만 입력하고 나머지를 빈칸으로 두면, 그 행(또는 열) 전체가 출력됩니다.
n<-rep(10,5)
o<-1:5
p<-cbind(n,o)
p
q<-rbind(n,o)
q
r<-matrix(1:4,2,2)
r
s<-matrix(c(1,4,2,7),2,2)
s
r+s
r%*%s
solve(s)
s[1,2]
s[1,]
s[,2]

연습문제
Q1. 다음 중 명목형 변수가 아닌 것은?
① 종교(천주교, 개신교, 불교, 기타)
② 혈액형(A, B, AB, O)
③ 비만도(저체중, 정상, 과체중, 비만)
④ 자동차 브랜드(현대, 기아, 르노삼성, 기타)
Q2. 다음 중 틀린 말은?
① 나이는 연속형 변수이지만 1년 단위로 기록할 경우 이산형 변수로도 볼 수 있다.
② 양적 변수와 질적 변수 모두 도수분포표로 정리할 수 있다.
③ 질적 데이터를 요약하는 가장 좋은 방법은 원그래프를 이용하는 것이다.
④ 히스토그램을 이용하면 특이점을 쉽게 찾아낼 수 있다.
정리하기
1. 변수는 질적 변수와 양적 변수로 나뉩니다. 질적 변수에는 명목형 변수, 순서형 변수가 있고, 양적 변수에는 연속형 변수와 이산형 변수가 있습니다.
2. 변수의 분포를 나타내기 위하여 각 값의 출현빈도나 비슷한 값끼리 묶은 구간별로 관측된 데이터의 개수를 정리한 표를 도수분포표라고 합니다.
3. 각 범주에 속한 관찰값의 개수 또는 비율을 막대의 길이로 나타낸 것을 막대그래프라고 합니다.